1. Поняття про статистичні ряди динаміки, їх значення. Види рядів динаміки, особливості побудови.
2. Показники аналізу динамічних рядів.
3. Середній рівень та середній темп зростання.
І. Поняття про статистичні ряди динаміки, їх значення.
Види рядів динаміки, особливості побудови.
Динамікою в статистиці прийнято називати процес розвитку, руху соціально-економічних явищ у часі. Для відображення і аналізу динаміки будують динамічні (хронологічні, часові) ряди. Дослідження динаміки дає змогу охарактеризувати процес розвитку явищ, розкрити основні шляхи, тенденції і темпи цього розвитку.
Ряд динаміки – ряд статистичних показників, які характеризують зміну суспільних явищ у часі.
Кожний ряд динаміки складається з двох обов’язкових елементів:
- періодів часу (t);
- рівнів (у).
Показники часу в рядах динаміки можуть бути:
- певні дати (моменти) часу;
- окремі періоди (роки, квартали, місяці, декади, доба).
Рівнем ряду динаміки називають статистичний показник, який характеризує величину суспільного явища на даний момент або за певний період часу. Вони відображають кількісну оцінку (міру) розвитку дослідженого суспільного явища.
Залежно від характеру рівнів ряду розрізняють два види рядів динаміки: інтервальні та моментні.
Моментними називають ряди динаміки, які характеризують розмір явища на певний період часу.
За допомогою моментних рядів динаміки характеризується найчастіше стан умов і факторів виробництва.
Інтервальними називають ряди динаміки, які характеризують розмір явищ за певний період часу.
За допомогою інтервальних динамічних рядів характеризуються підсумки виробничого процесу (обсяги виробленої продукції, виконаних робіт, затрат праці, кількості внесених добрив тощо).
За кількістю показників, що змінюються, ряди динаміки бувають одновимірні та багатовимірні.
Якщо ряд динаміки характеризує зміну одного по¬казника, то його називають одномірним, двох і більше - багатомірним. Багатомірні ряди бувають двох видів: паралельні ряди та ряди взаємозв'язаних показ¬ників.
Паралельні характеризують динаміку або одного показника щодо різних об'єктів, або різних показників щодо одного об'єкта. Зв'язок між показниками багатомірного динамічного ряду може бути функціо¬нальним або кореляційним.
За повнотою часу динамічни ряд поділяються на повні й неповні.
У повних динамічних рядах дати або періоди ідуть один за одним з рівними інтервалами.
У неповних динамічних рядах у послідовності показників спостерігають нерівні часові інтервали.
За способом вираження рівнів динамічні ряди поділяються на ряди абсолютних, відносних та середніх величин.
У динамічних рядах потрібно дотримуватися порівнянності всіх рядів між собою за територією, методикою розрахунку показників, періодом, або моментом часу, об’єктом і одиницею спостереження, ступенем охоплення одиниць досліджуваної сукупності, одиницями вимірювання.
Непорівнянність даних, що виникає внаслідок адміністративно-територіальних змін, часто виявляється в статистичній практиці. Це зумовлено тим, що межі територій господарств, районів, областей протягом досліджуваного періоду змінюються внаслідок приєднання до них нових територій або від'єднання окремих частин їхньої території. Для приведення даних до порівнянного виду необхідно виконати перерахунок даних за попередні роки (до зміни території) з урахуванням І нових меж.
Найбільш суттєвою вимогою при побудові ряду динаміки є єдина методика обчислення рівня за кожний з періодів, що розглядається. Завдяки цьому забезпечується порівнянність статистичних показників за змістом.
Наприклад, при вивченні динаміки урожайності сільського¬сподарських культур показник урожайності повинен відноситись до однієї і тієї самої посівної площі (весняної продуктивної, фактично зі¬браної і т.д.). При дослідженні динаміки вартісних показників обсягу продукції необхідно усунути вплив зміни цін. На практиці для вирі¬шення цього завдання кількість продукції, виробленої в різні періоди, оцінюють в цінах одного періоду, які називають фіксованими, або по¬рівнянними. Якщо ряд динаміки подано узагальнюючими показниками в умовно-натуральних одиницях вимірювання, коефіцієнти сумірництва для всіх рівнів мають бути єдиними.
Порівнянність рівнів ряду динаміки за періодом, або моментом спостереження, означає, що:
1) всі показники характеризують явище або за певний період часу, або на певний момент часу. В зв'язку з цим неправомірно порівнювати, наприклад, середньорічне число тракторів з числом тракторів на початок або кінець року;
2) в інтервальних динамічних рядах рівні повинні відноситись до рівних періодів часу, а в моментних - повинні бути, як правило, рівні відрізки часу між моментами (датами) спостереження. Крім того, не можна поєднувати в одному ряду динаміки періоди і моменти часу.
Порівнянність за об'єктом спостереження означає, що всі рівні ряду динаміки відносяться до одного і того самого об'єкта спостереження. Наприклад, при дослідженні динаміки продуктивності корів об'єктом спостереження можуть бути державні, колективні, фермерські господарства, особисті підсобні господарства населення або всі катего¬рії в цілому. Для одержання порівнянної в динаміці продуктивності корів показник повинен розраховуватись по одній і тій самій категорії господарства або по їх сукупності.
Порівнянність за одиницями спостереження передбачає, що всі рівні одержані по одних і тих самих одиницях спостереження. Одиницями спостереження можуть бути окремі підприємства або їхні під¬розділи. Наприклад, при вивченні динаміки урожайності сільськогосподарських культур показник урожайності повинен визначитися по одних і тих самих сільськогосподарських підприємствах, фермах і т.д.
Крім перелічених вимог, без урахування яких неможливо побудувати ряд динаміки, потрібно дотримуватися одних і тих самих оди¬ниць вимірювання. Так, якщо дані про валовий збір за одні роки наводяться в тонах, а за інші - в центнерах, то необхідно перерахувати весь ряд в одні і ті самі одиниці вимірювання.
Науково обґрунтоване формування рядів динаміки вимагає також виділення строго однорідних періодів (етапів) у розвитку досліджуваних соціально-економічних явищ, тому що всебічного аналізу динамі¬чних процесів можна досягти лише в межах однорідних періодів. Пе¬ріодизацію динамічних рядів слід проводити на основі глибокого тео¬ретичного аналізу основних процесів і законів, які визначають розви¬ток досліджуваного явища.
Особливості періодичного ряду по відношенню з моментним.
1. Рівні інтервального ряду можна складати , отримуя при цьому новий ряд, але за більш довший відрізок часу. Цю особливість використовують в статистичній звітності.
2. Рівні інтервального ряду залежать від величини періоду або відрізку часу.
ІІ. Показники аналізу динамічних рядів.
Для опису рядів динаміки визначають абсолютні та відносні характеристики динаміки: абсолютний приріст та абсолютне значення 1% приросту; темп зростання та темп приросту.
Обчислення характеристик ґрунтується на співставленні рівнів ряду.
Якщо базою при цьому є попередній рівень, то вона називається змінною, а самі характеристики - ланцюговими. Якщо ж за базу обраний початковий рівень Уо, то базу називають постійною, а характеристики базисними.
Абсолютний приріст - характеризує розмір збільшення(зменшення) рівня ряду за певний період. Обчислюється як різниця між поточним і базисним рівнями, щоб знайти на скільки одиниць підвищився чи зменшився рівень щодо базисного за певний період часу.

Абсолютний приріст виражає абсолютну швидкість зміни рівнів ряду динаміки. Для вичерпної та глибокої характеристики явища абсолютні величини доповнюють відносними.
Абсолютний приріст може мати додатний або від’ємний знак. Якщо наступний рівень ряду динаміки більший за попередній, то абсолютний приріст буде мати знак «+», якщо менше – знак «-».
Темп (коефіцієнт) зростання Кt обчислюється як відношення зіставлюваного рівня з рівнем, прийнятим за базу зіставлення, і показує, в скільки разів (процентів) порівнюваний рівень більший чи менший від базисного.
Темп зростання може бути виражений у вигляді коефіцієнтів або процентів. Темп зростання, виражений у процентах, називають процентом зростання.
Величина темпу зростання буде більшою від одиниці, якщо рівень щодо бази порівняння зростає, і меншою за одиницю, якщо рівень щодо бази порівняння зменшується.

Між ланцюговими і базисними темпами зростання існує певний взаємозв'язок:
а) добуток ланцюгових темпів зростання дорівнює базисному темпу зростання за відповідний період;
б) частка від ділення двох сусідніх базисних коефіцієнтів зростання дорівнює відповідному ланцюговому коефіцієнту зростання.
Взаємозв'язок ланцюгових та базисних темпів зростання використовують для переходу від одних темпів зростання до інших у тих випадках, коли невідомі абсолютні рівні ряду динаміки.
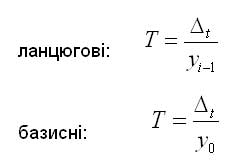
Поряд з темпами зростання відносна зміна явища у часі може бути також охарактеризована за допомогою темпів приросту (Т).
Темп приросту - це відношення абсолютного приросту до абсолютного попереднього або початкового рівня і показує, на скільки процентів порівнюваний рівень більший або менший від рівня, взятого за базу порівняння:

Темп приросту, як і абсолютний приріст, може бути як додатним, так і від'ємним числом (відповідно при зростанні і зниженні рівня) і виражається у вигляді коефіцієнтів або процентів. На практиці темпи приросту найчастіше виражаються у формі процентів.
Вони показують, на скільки процентів збільшився або зменшився поточний рівень порівняно з базисним, взятим за 100%.
Між темпом зростання і темпом приросту існує зв'язок:

тобто темп приросту завжди на одиницю менше відповідного темпу зростання, вираженого у формі коефіцієнта, або на 100%, якщо його виражено в процентах.
Абсолютне значення одного процента приросту А% можна знайти шляхом ділення абсолютного приросту на темп приросту за один і той самий період. Абсолютне значення одного процента приросту можна обчислити простішим способом — діленням початкового рівня на 100, оскільки за 100 % завжди беруть базисний рівень, то 1 % буде в 100 разів менший від базисного рівня:

Цей показник дає змогу визначити вагомість кожного проценту приросту, і те, яка абсолютна величина приховується за цим процентом.
Розрахунок цього показника має економічний зміст тільки на ланцюговій основі, оскільки на базисній основі по всіх часових відрізках буде отримано одне і те саме значення показника - сота частина початкового (першого) рівня.
ІІІ. Середній рівень та середній темп зростання.
Динамічні ряди складаються з багатьох варіаційних рівнів, а тому, як будь-яка статистична сукупність, вони потребують деяких узагальнювальних характеристик. Для цього обчислюють середні показники: середні рівні ряду, середні абсолютні прирости, середні темпи зро¬стання і приросту.
Методи обчислення середнього рівня інтервального і моментного рядів динаміки залежать від їхнього вигляду.
В інтервальних рядах з рівними інтервалами середній рівень ряду обчислюють за формулою середньої арифметичної простої:

Якщо інтервальний ряд ряд динаміки має нерівновіддалені один від одного рівні, то середній рівень розраховується за формулою середньої арифметичної зваженої:

У моментному ряду з рівними відрізками часу середній рівень обчислюється як середня хронологічна:

У знаменнику від числа рівнів віднімають одиницю, оскільки в чисельнику серед доданків перший і останній рівні беруть в половинному розмірі.
Якщо окремі періоди інтервального ряду динаміки мають різну довжину, то для визначення середнього рівня використовують середню арифметичну зважену:

Середній абсолютний приріст визначають як середню арифме¬тичну просту з ланцюгових абсолютних приростів за певні періоди, знаходять, на скільки одиниць у середньому змінився рівень порівняно з попереднім.

Для узагальнюючої характеристики темпів зростання за ряд років об¬числюють середній темп (коефіцієнт) зростання ( ). Він показує, в скільки разів у середньому кожен даний рівень ряду більший (або менший) від попереднього рівня. Для динамічних рядів з рівними проміжками між датами середній темп зростання обчислюється за формулою середньої геометричної:

Питання для закріплення знань:
1. Що характеризує собою ряд динаміки?
2. Які ряди динаміки називають моментними і чому їхні рівні не можна підсумовувати?
3. Чим відрізняється моментний ряд від інтервального?
4. Як обчислити середній рівень моментного ряду?
5. Як визначити абсолютний приріст? Як визначити темп зростання?
6. У чому полягає різниця базисного і ланцюгового способів обчислення показників динаміки?
7. Які види середніх використовуються для визначення середнього рівня ряду динаміки?
Література:
Основна:
1. Уманець Т.В., Пигарев Ю.Б. Статистика, Київ, «Викар», 2003.с. 153-163
2. Гусаров В.М. Теория статистики, М, Аудит, 1998. с. 119-142
Додаткова:
1. Ковтун Н . В ., Столяров Г.С. Загальна теорія статистики, Київ, "Четверта хвиля", 1996р. с. 97-204
2. Мармоза А.Т. Теорія статистики. - К.: Ельга, Ніка-Центр, 2003. с. 262 - 275
3. Спирина А. А., Башина 0.3. Общая теория статистики, М ., Фінанси і статистика, 1997р. с.221-239
